航空发动机涡轮叶片有限元分析
在叶片盘结构的分析中,其几何形状、施加的载荷以及边界条件都围绕涡轮的旋转轴呈现出精确的对称性。可以采用循环对称假设来降低计算负荷。利用对称性,可先将有限元模型的范围缩小到单个扇形区域进行分析,然后将该扇形区域的分析结果扩展到其他扇形区域,从而得到整个系统的结果。因此,为了构建有限元模型并进行必要的分析,对占整个系统 1/60 的、包含两个叶片的涡轮扇形区域进行了建模。

图1 带叶根阻尼器的完整叶片盘
有限元模型所考虑的扇形区域由两个叶片、叶根阻尼器、枞树形榫头、轮盘部件以及这些部件之间的接触组成,如图 2 所示。有限元模型包含 171,523 个 SOLID185 单元、85,932 个节点和 257,796 个自由度。此外,总共为接触区域分配了 5,512 个接触节点,这些节点通过库仑摩擦模型相互关联。叶片与阻尼器之间以及枞树形榫头与轮盘之间的接触界面如图 3 所示。
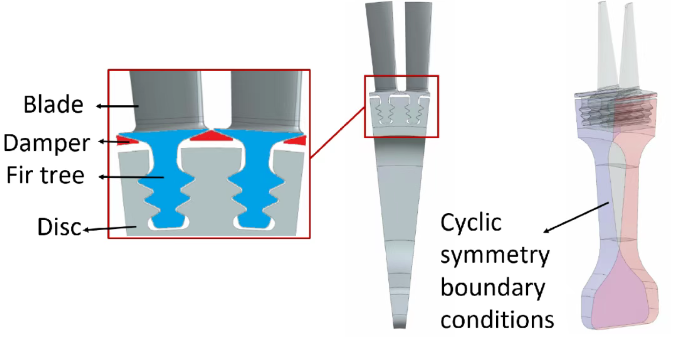
图2 用于构建有限元模型的几何形状
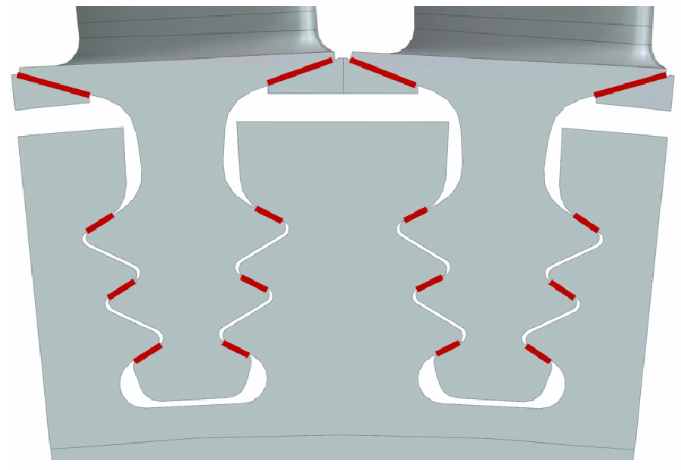
图3 接触表面
静态分析
静态分析旨在考虑静态载荷和条件的影响,以便从模态分析和时域动态仿真中获得更精确的结果。在本示例中,静态模型考虑了循环对称性,并考虑了稳态温度分布对材料属性的影响、5000 转 / 分钟的旋转体力以及作用在叶片上的静态气动力压力载荷和作用在压力面与吸力面上的压力载荷。
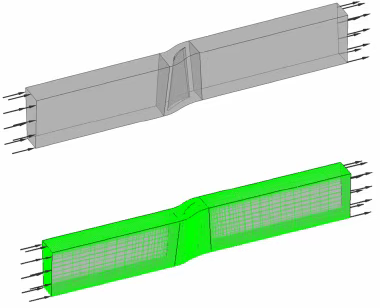
图4 稳态气动力压力载荷和温度场

图5 作用在叶片上的静态压力载荷
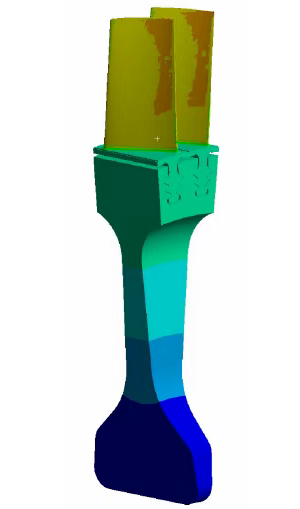
图6 叶片盘系统稳态下的温度分布
模态分析
静态分析完成后,通过模态分析研究结构的动态行为,以确定固有频率和振型。该模态分析考虑了机械载荷、温度和旋转体力的综合影响,并将静态分析的结果作为预应力纳入其中。主要通过求解特征值问题得到的结果,反映了在这些条件下结构的动态特性。
图 7 展示了 0 阶谐波指数 / 节径下的前六阶振型,清晰地说明了系统的循环对称性在其振动模态中的体现。
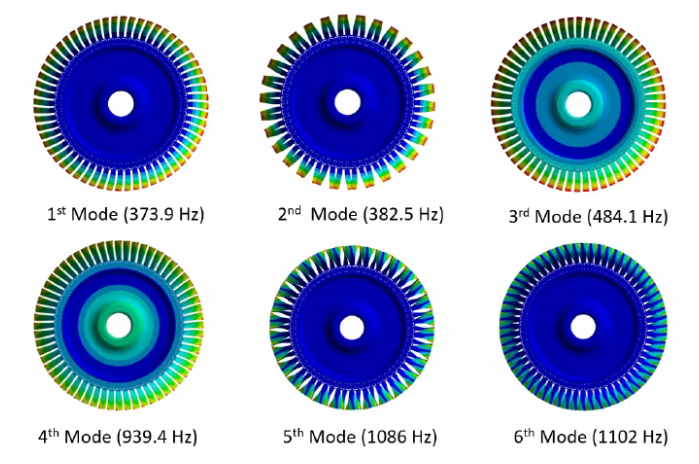
图 7 :存在叶根阻尼器时,0 阶谐波指数 / 节径下的前六阶振型
第一阶模态的特征是所有叶片同步挥舞运动,在叶片尖端产生最大挠度。这一模态至关重要,因为它通常具有最低的频率,在运行过程中很容易被激发。第二阶模态代表反相挥舞,相邻叶片向相反方向运动,有效地抵消了部分系统的整体位移,并可能降低轮盘上的应力。
对于第三阶和第四阶模态,存在单个节圆表明涉及轮盘模态,这表明存在更复杂的振动行为。这些叶片模态涉及挥舞和扭转的组合。这些模态很重要,因为它们会导致轮盘上的不对称加载,影响其疲劳寿命。第五阶和第六阶模态又回到 0 节圆,表明叶片运动更加复杂,分别是反相和同相的耦合叶片弯曲 - 扭转模态。

