有限元法(Finite Element Method, FEM)是一种基于数值计算的工程分析技术,广泛应用于机械工程领域,用于解决复杂的结构、热力学、动力学等问题。
1. 结构强度与刚度分析(如图1)
应用场景:
应力与变形计算:分析机械零件(如轴、齿轮、连杆)或整体结构(如桥梁、飞机机身)在载荷作用下的应力分布和变形。
安全评估:通过比较最大应力与材料屈服强度,判断设计是否满足安全要求。
2. 疲劳与寿命预测(如图2)
应用场景:
循环载荷分析:模拟机械部件(如发动机曲轴、螺栓)在反复载荷下的损伤累积,预测疲劳裂纹萌生位置和寿命。
3. 振动与动力学分析(如图3)
应用场景:
模态分析:计算结构的固有频率和振型,避免共振(如机床主轴、涡轮机转子)。
谐响应分析:分析结构在周期性载荷(如电机振动)下的动态响应。
4. 热力学与热应力分析(如图4)
应用场景:
温度场模拟:预测设备(如发动机缸体、电子芯片)在热载荷下的温度分布。
热变形与应力:分析因温度梯度导致的热膨胀/收缩(如焊接变形、刹车盘热应力)。
5. 接触与摩擦分析
应用场景:
接触应力计算:分析齿轮啮合、轴承滚子与轨道间的接触压力分布。
摩擦磨损预测:优化表面处理工艺以减少磨损(如活塞环与气缸壁)。
6. 优化设计
应用场景:
拓扑优化:通过材料分布优化实现轻量化(如飞机桁架、汽车骨架)。
形状优化:调整几何形状以降低应力集中(如过渡圆角设计)。
7. 制造工艺模拟
应用场景:
成型过程分析:预测铸造、锻造、注塑等工艺中的缺陷(如缩孔、回弹)。
残余应力预测:评估焊接、热处理后的残余应力分布。
8. 多物理场耦合分析
应用场景:
流固耦合(FSI):分析流体与结构的相互作用(如风力涡轮叶片的气动弹性)。
热-结构耦合:研究温度场与机械场的相互影响(如制动系统热衰退)。
9. 复合材料与非线性材料分析
应用场景:
各向异性材料:分析纤维增强复合材料(如碳纤维车身)的层间失效。
非线性行为:模拟橡胶密封件的超弹性变形或金属塑性成形。
10. 生物力学与医疗器械设计
应用场景:
植入物力学分析:优化人工关节(如髋关节假体)的受力分布。
生物组织模拟:研究骨骼、肌肉在载荷下的响应。
有限元法的核心优势
复杂问题简化:将连续体离散为有限单元,适用于任意几何形状。
成本与时间节约:减少物理试验次数,缩短产品开发周期。
多学科融合:支持结构、热、流体、电磁等多物理场耦合仿真。
高精度预测:结合材料非线性、边界条件非线性,提供高可信度结果。

图1汽车底盘的承载能力分析
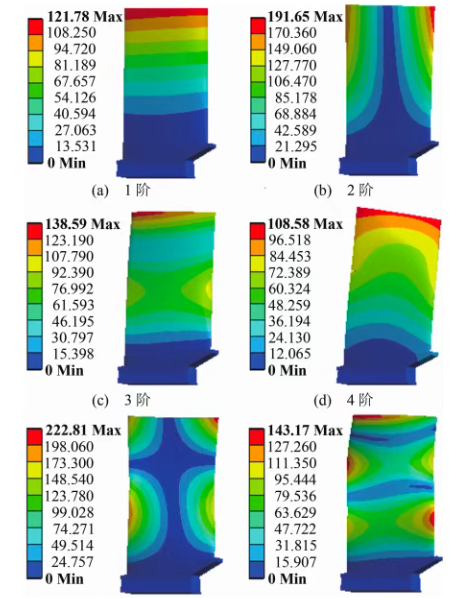
图2航空发动机叶片的高周疲劳分析
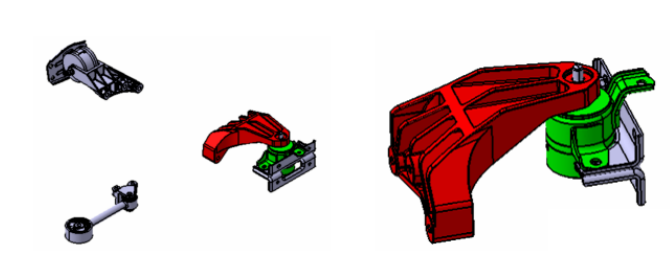
图3汽车悬架系统的减振优化
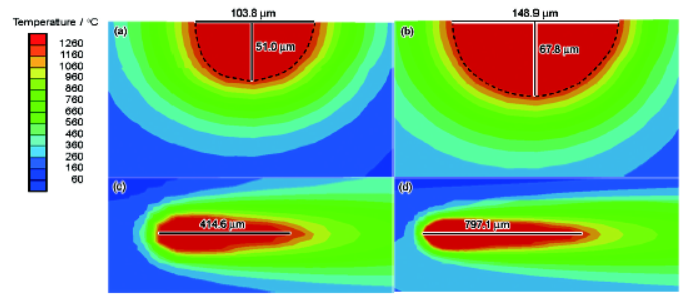
图4激光切割过程中的热影响区分析

